Question

Polygon ABC D is dilated rotated and translated to form polygon a prime be prime see prime see the prime the endpoints of a B are at zero and -7 and eight and eight in the endpoints of a prime be prime or at six and -6 and two and 1.5 what is the scale factor of the dilation

Answer 1

`\frac12`

Explanation:

The endpoints AB are at (0,-7) and (8,8)

The endpoints A'B' are at (6,-6) and (2,1.5)

To determine the scale factor of the dilation, we determine the lengths of the segments AB and A'B' using the distance formula.

`AB=\sqrt{(8-0)^(2)+(8-(-7))^(2)}\\=\sqrt{8^(2)+15^(2)}\\=√(64+225)\\=√(289)\\AB=17`

`A^(\prime) B^(\prime)=\sqrt{(2-6)^(2)+(1.5-(-6))^(2)}\\=\sqrt{4^(2)+7.5^(2)} \\=√(16+56.25)\\=√(72.25)\\A'B'=8.5`

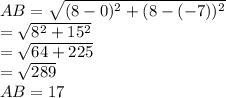
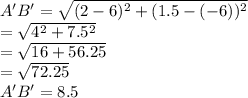
Length of AB in the pre-image = 17 Units

Length of AB in the image, A'B'=8.5 Units

Therefore, the scale factor of the dilation

=
`(8.5)/(17)=\frac12`