Answer:
x = 42.2 units
Explanation:
By applying tangent rule in the right triangle ΔADC,
tan(44)° =
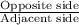
0.9657 =
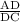
0.9657 =
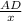
AD = 0.9657x
Now we apply cosine rule in ΔADB,
cos(30)° =
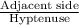
cos(30)° =
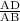
0.866 =
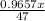
x =
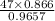
x = 42.15
x ≈ 42.2 units
Therefore, x = 42.2 units will be the answer.