Question

A political candidate has asked you to conduct a poll to determine what percentage of people support her. If the candidate only wants a 4% margin of error at a 99% confidence level, what size of sample is needed? Give your answer in whole people.

Answer 1

Explanation:

Hello!

The variable of interest is:

X: Number of people that support the candidate.

You need to calculate the sample size to estimate the population proportion of supporters given a confidence level of 99% and a margin of error of 4%

The margin of error of the confidence level for the population proportion is

d=
`Z_(1-\alpha /2)` *
`\sqrt{(p'(1-p'))/(n) }`

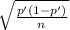
From this formula you have to clear the value of n:

`(d)/(Z_(1-\alpha /2))`=
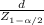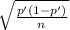
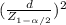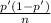
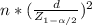`\sqrt{(p'(1-p'))/(n) }`

`((d)/(Z_(1-\alpha /2)))^2`=
`(p'(1-p'))/(n)`

`n*((d)/(Z_(1-\alpha /2)))^2`=
`p'(1-p')`

n=
`p'(1-p') * ((Z_(1-\alpha/2))/(d) )^2`

`Z_(1-\alpha/2)= Z_(0.995)= 2.586`

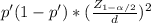
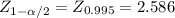
sample proportion "p'" since there is no sample information, nor any previous information is known, you have to consider it as the "worse case scenario" and use the value of p'= 0.50

d= 0.04

`n= p'(1-p') * ((Z_(1-\alpha/2))/(d) )^2= 0.5*0.5*((2.586)/(0.04) )^2= 1044.9= 1045`

She has to take a sample of 1045 people to estimate the population proportion of her supporters with a confidence level of 99% and a margin of error of 4%

I hope this helps!