Answer:
A) g(x) has a greater absolute maximum.
Explanation:
Given graph of g(x) which is a Parabola
1. Opens downwards
2. The absolute maximum (vertex) is at around (3.5, 6)
i.e. value of absolute maximum is 6.
Another function:

Let us convert it to vertex form to find its vertex.
Taking - sign common:
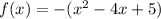
Now, let us try to make it a whole square,
Writing 5 as 4+1:
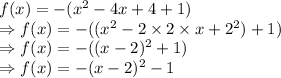
Please refer to attached graph of f(x).
We know that, vertex form of a parabola is given as:
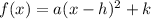
Comparing the equations we get:
a = -1 (Negative value of a means the parabola opens downwards)
h = 2, k = -1
Vertex of f(x) is at (2, -1) i.e. value of absolute maximum is -1
and
Vertex of g(x) is at (3.5, 6)
i.e. value of absolute maximum is 6.
Hence, correct answer is:
A) g(x) has a greater absolute maximum.