Answer:
(a)Exponential
(b)
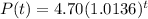
(c)The price of milk next year will be: $4.76
(d)5 years
Explanation:
The price of a gallon of milk has been rising about 1.36% per year since 2000.
(a)Since the price grows by a percentage (or constant factor) each year, an exponential function would be best to model the scenario.
(b)The exponential growth model is given as:
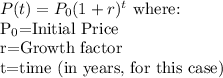
The independent variable in the function is t. This represents the number of years since 2000.
(c)
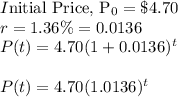
Therefore, the price of milk next year will be:
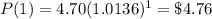
(d)We want to determine how long it will take for the price to top $5.
P(t)=$5
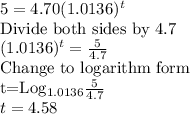
Therefore, in exactly 4.58 years, the milk price would be $5. Therefore, by the 5th year, the milk price would top $5.