Question

Flying against the wind, an airplane travels 7520 kilometers in 8 hours. Flying with the wind, the same plane travels 6500 kilometers in 5 hours. What is the rate of the plane in still air and what is the rate of the wind?

Answer 1

Rate of plane in still air = 1120 km/h

Rate of wind = 180 km/h

Explanation:

Let the rate (speed) of the plane in still air = u km/h

Let the rate (speed) of the wind = v km/h

Formula for speed is:

`Speed = (Distance)/(Time)`

Given that against the wind, airplane travels 7520 km in 8 hours.

The speed against the wind will be slower so,

Against the wind, speed = (u -v ) km/h

Using above formula:

`(u-v) = (7520)/(8) km/h\\(u-v) = 940 km/h ..... (1)`

Given that with the wind, airplane travels 6500 km in 5 hours.

The speed with the wind will be faster so,

With the wind, speed = (u +v ) km/h

Using above formula:

`(u+v) = (6520)/(5) km/h\\(u+v) = 1300 km/h ..... (2)`

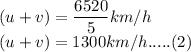
Adding (1) and (2) to solve for u and v:

`2u = 2240\\\Rightarrow u = 1120\ km/h`

Putting u in (1):

`1120-u=940\\\Rightarrow u = 180\ km/h`

So, the answers are:

Rate of plane in still air = 1120 km/h

Rate of wind = 180 km/h