Question

A parallel-plate capacitor with circular plates of radius R is being discharged. The displacement current through a central circular area, parallel to the plates and with radius R/2, is 9.2 A. What is the discharging current?

Answer 1

The discharging current is
`I_d = 36.8 \ A`

Step-by-step explanation:

From the question we are told that

The radius of each circular plates is R

The displacement current is
`I = 9.2 \ A`

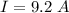
The radius of the central circular area is
`(R)/(2)`

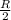
The discharging current is mathematically represented as

`I_d = (A)/(k) * I`

where A is the area of each plate which is mathematically represented as

`A = \pi R ^2`

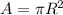
and k is central circular area which is mathematically represented as

`k = \pi [(R)/(2) ]^2`

So

`I_d = (\pi R^2 )/(\pi * [ (R)/(2)]^2 ) * I`

`I_d = (\pi R^2 )/(\pi * (R^2)/(4) ) * I`

`I_d = 4 * I`

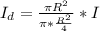
substituting values

`I_d = 4 * 9.2`

`I_d = 36.8 \ A`