Answer:
The equation is
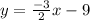
Explanation:
First, you will have to find the slope of the two points.To do that, you will have to use the formula :
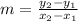
Our points are
 and
and

We will have to substitute the points into the formula.
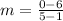
Then, we will simplify
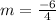
We could simplify that fraction into
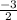
So, our slope is
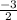
We will have to pick a coordinate point, and choose. I chose

We will substitute the x-value and the y-value of the coordinate point, including our slope, to calculate the y-intercept.
The formula we will be using is

We will substitute in our values which will make it look like:
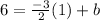
We will then multiply
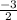 by
by
 which will stay the same.
which will stay the same.
Then, we will multiply
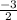 by
by
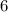 which will equal
which will equal
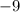
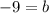
Hence, the equation for our line is
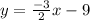
Hope it helped:D
-Jazz