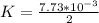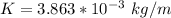Answer:
The linear density is
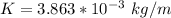
Step-by-step explanation:
From the question we are told that
The density of steel is
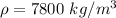
The diameter of the string is
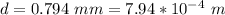
The radius of the string is evaluated as
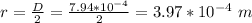
The volume of the string is mathematically evaluated as
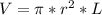
Now assuming that the length of the string is L = 2 m
So
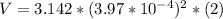

Then the mass of the string would be
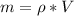
substituting value
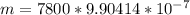
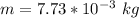
Looking at the question we see that the unit of the linear density is
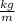
Hence the linear density is evaluated as
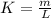
substituting value