Question

g 7. Find Re f and Im f and find their values at the given z. (Both answers should be included) f = z⁄(z + 1), z = 4 − 5

Answer 1

The real and imaginary parts of the result are
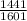`(1441)/(1601)` and
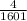`(4)/(1601)`, respectively.

Explanation:

Let be
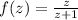`f(z) = (z)/(z+1)`, the following expression is expanded by algebraic means:

`f(z) = (z\cdot (z-1))/((z+1)\cdot (z-1))`

`f(z) = (z^(2)-z)/(z^(2)-1)`

`f(z) = (z^(2))/(z^(2)-1)-(z)/(z^(2)-1)`

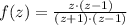
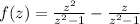
If
`z = 4 - i5`, then:

`z^(2) = (4-i5)\cdot (4-i5)`

`z^(2) = 16-i20-i20-(-1)\cdot (25)`

`z^(2) = 41 - i40`

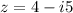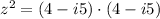
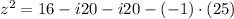
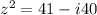
Then, the variable is substituted in the equation and simplified:

`f(z) = (41-i40)/(41-i39) -(4-i5)/(41-i39)`

`f(z) = (37-i35)/(41-i39)`

`f(z) = ((37-i35)\cdot (41+i39))/((41-i39)\cdot (41+i39))`

`f(z) = (1517-i1435+i1443+1365)/(3202)`

`f(z) = (2882+i8)/(3202)`

`f(z) = (1441)/(1601) + i(4)/(1601)`

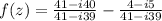
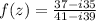
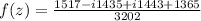
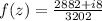
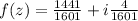
The real and imaginary parts of the result are
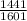`(1441)/(1601)` and
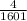`(4)/(1601)`, respectively.