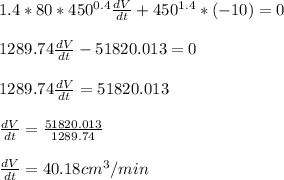Question

When air expands adiabatically (without gaining or losing heat), its pressure P P and volume V V are related by the equation P V 1.4 = C PV1.4=C, where C C is a constant. Suppose that at a certain instant the volume is 450 cm 3 450 cm3 and the pressure is 80 kPa 80 kPa and is decreasing at a rate of 10 kPa/min 10 kPa/min. At what rate is the volume increasing at this instant? (Round your answer to the nearest whole number.)

Answer 1

Rate at which the volume is increasing,
`(dV)/(dt) = 40.18 cm^3/min`

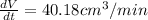
Step-by-step explanation:

Volume, V = 450 cm³

Pressure, P = 80 kPa

Rate of decrease in pressure,
`(dP)/(dt) = - 10 kPa/min`

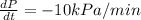
Rate of increase in volume,
`(dV)/(dt) = ?`

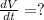
The equation relating the pressure, P and the volume,V

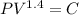`PV^(1.4) = C`..............(1)

Differentiating both sides with respect to t (Using Products rule)

`1.4 PV^(0.4) (dV)/(dt) + V^(1.4) (dP)/(dt) = 0`..............(2)

Substitute the necessary parameters into equation (2)

`1.4 * 80*450^(0.4) (dV)/(dt) + 450^(1.4) *(-10) = 0\\\\1289.74 (dV)/(dt) - 51820.013 = 0\\\\1289.74 (dV)/(dt) = 51820.013\\\\(dV)/(dt) = (51820.013)/(1289.74)\\\\(dV)/(dt) = 40.18 cm^3/min`