Answer:
1125 m
Explanation:
Given equation:
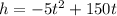
where:
- h = height (in metres)
- t = time (in seconds)
Method 1
Rewrite the equation in vertex form by completing the square:
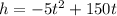
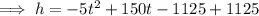

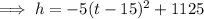
The vertex (15, 1125) is the turning point of the parabola (minimum or maximum point). As the leading coefficient of the given equation is negative, the parabola opens downward, and so vertex is the maximum point. Therefore, the maximum height is the y-value of the vertex: 1125 metres.
Method 2
Differentiate the function:
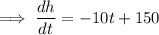
Set it to zero and solve for t:
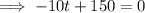
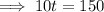

Input found value of t into the original function and solve for h:
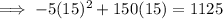
Therefore, the maximum height is 1125 metres.