Question

Which set of data is correct for the quadratic relation f(x) = 5(x -

27)2 - 9?
3
6
A.
B.
C.
D.
Direction parabola opens
upward
downward
upward
downward
Vertex
(27, 9)
(-27,9)
(-27, -9)
(27,9)
Axis of Symmetry
x=27
x = -27
x = -9
x=9
Set A
Set B
Set C
Set D

Answer 1

Direction parabola opens upward.

Vertex of parabola is (27,-9).

Axis of symmetry is
`x=27`.

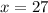Explanation:

Note: Option sets are not correct.

The vertex form of a parabola is

`y=a(x-h)^2+k` ...(1)

where, (h,k) is vertex and x=h is the axis of symmetry.

If a<0, then parabola opens downward and if a>0, then parabola opens upward.

The given function is

`f(x)=5(x-27)^2-9` ...(2)

On comparing (1) and (2), we get

`a=5>0`, so direction parabola opens upward.

`h=27,k=-9`, so vertex of parabola is (27,-9).

So, axis of symmetry is
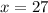`x=27`.