Answer:
1) The magnitude of force that the worker must apply is 47.074 newtons, 2) The work done by the worker's push is 230.663 joules, 3) The work done by friction is -230.661 joules, 4) The work done by normal force is 0 joules, 5) The net work done on the crate is 0 joules.
Step-by-step explanation:
1) The magnitude of the force that worker must apply must be equal to the kinetic friction force between the crate and the floor. (Newton's Third Law) As the box moves at constant velocity, net force of the system must be zero. (Newton's Second Law). The equations of equilibrium for the crate are, respectively:
(Parallel to ground)
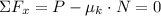
(Perpendicular to ground)

Where:
 - Force exerted on the crate by the worker, measured in newtons.
- Force exerted on the crate by the worker, measured in newtons.
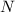 - Normal force, measured in newtons.
- Normal force, measured in newtons.
 - Mass of the crate, measured in kilograms.
- Mass of the crate, measured in kilograms.
 - Gravitational constant, measured in meters per square second.
- Gravitational constant, measured in meters per square second.
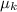 - Coefficient of kinetic friction, dimensionless.
- Coefficient of kinetic friction, dimensionless.
The magnitude of the force is obtained after reducing the system of equations and replacing every known variable:

If
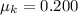 ,
,
 and
and
 , the magnitude of the force is:
, the magnitude of the force is:

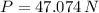
The magnitude of force that the worker must apply is 47.074 newtons.
2) As force is constant and parallel to motion, the work done on the crate by the worker is calculated by multiplying the force by the travelled distance:
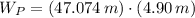
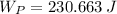
The work done by the worker's push is 230.663 joules.
3) Friction force is constant and antiparallel to motion. The work done by the friction is equal to the product of the friction force and the travelled distance. That is:
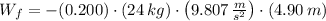

The work done by friction is -230.661 joules.
4) Since normal force is perpendicular to motion. The work done by the normal force is zero.
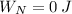
The work done by normal force is 0 joules.
5) The net work done on the crate is equal to the following sum:
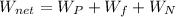
If
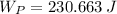 ,
,
 and
and
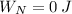 , the net work done on the crate is:
, the net work done on the crate is:
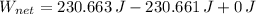
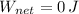
The net work done on the crate is 0 joules.