Question

A grandfather clock (with a pendulum) keeps perfect time on Earth. If you were to transport this clock to the Moon, would its period of oscillation increase, decrease, or stay the same? Would its frequency of oscillation increase, decrease, or stay the same? Explain.

Answer 1

a) Therefore the period of oscillation in the moon will increase.

`T_(E)<T_(M)`

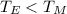
b) The frequency in the moon will decrease

`\omega_(E)>\omega_(M)`

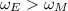
Step-by-step explanation:

The period of the pendulum is given by this equation:

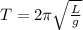`T=2\pi\sqrt{(L)/(g)}` (1)

As we can see, T is proportional to L and inversely proportional to the gravity vector. We know that g in the earth is grader than g in the moon.

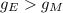`g_(E)>g_(M)` (2)

Therefore the period of oscillation in the moon will increase.

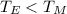`T_(E)<T_(M)` (3)

Now, the frequency of oscillation is:

`\omega=\sqrt{(g)/(L)}`

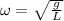
In this case, ω is proportional to g, then using (1) we can conclude that:

`\omega_(E)>\omega_(M)`

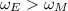
Therefore the frequency in the moon will decrease.

I hope it helps you!

Answer 2

Frequency of oscillation will increase

Step-by-step explanation:

Because The period of a pendulum is inversely proportional to the square root of the gravitational acceleration, so as. Gravity increases on the moon period of oscillation decreases whereas period of oscillating pendulum is inversely proportional to frequency thus frequency is directly proportional to gravity so as gravity increases on the moon the frequency will increase