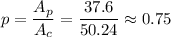Question

Acellus

Find the probability that a

randomly selected point within the

circle falls in the red shaded area.

r = 4 cm

ba = 3.2 cm

S = 4.7 cm

p = [?]

Enter a decimal rounded to the nearest hundredth.

Enter

Copyright © 2003-2000 Avellus Corporation. All Rights Reserved

No

Answer 1

The probability that a randomly selected point within the circle falls in the red shaded area is p=0.75.

Explanation:

We have to calculate the probability that a randomly selected point within the circle falls in the red shaded area.

This probability can be calculated as the quotient between the red shaded area, that is a regular pentagon inscribed in the circle, and the area of the circle.

We start by calculating the area of the circle:

`A_c=\pi r^2\approx 3.14(4)^2=3.14\cdot 16=50.24`

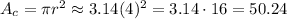
Then, we can calculate the area of the pentagon as:

`A_p=(1)/(2)\cdot (5a)\cdot S=(1)/(2)\cdot (5\cdot3.2)\cdot 4.7=37.6`

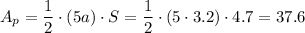
Then, we can calculate the probability p as the quotient between the areas:

`p=(A_p)/(A_c)=(37.6)/(50.24)\approx 0.75`