Question

rectangle ABCD and DEFG are similar. if AB is 6, DE is 15, DG is 21, what is the length of AD, rounded to the nearest tenth?

Answer 1

Length of AD is 8.4 units.

Explanation:

Given that:

There are two similar rectangles ABCD and DEFG.

AB = 6 units

DE = 15 units

DG = 21 units

To find:

AD = ?

Solution:

Please refer to the attached image for having a look at the two given rectangles.

First of all, let us learn about the similar rectangles.

If two rectangles are similar, then the ratio of their corresponding sides are always equal.

i.e.

`(AB)/(AD) = (DE)/(DG)`

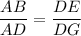
Putting values of AB, DE and DG to find out AD:

`(6)/(AD) = (15)/(21)\\\Rightarrow (6)/(AD) = (5)/(7)\\\Rightarrow (1)/(AD) = (5)/(7* 6)\\\Rightarrow (1)/(AD) = (5)/(42)\\\Rightarrow AD = (42)/(5)\\\Rightarrow AD = 8.4\ units`

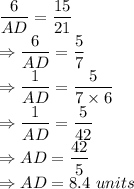
So, value of AD is 8.4 units.