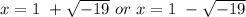Question

Using the quadratic formula to solve x2 + 20 = 2x, what are the values of x?

-1 IN
-10V21
19;
1+2 V19;
1+ 19/

Answer 1

`x = 1 \ + √(-19)\ or\ x = 1 \ - √(-19)`

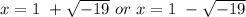
Explanation:

Given

`x^2 + 20 = 2x`

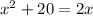
Required

Solve using quadratic formula

We start by representing the above equation property

`x^2 + 20 = 2x`

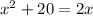
Subtract 2x from both sides

`x^2 + 20 - 2x= 2x - 2x`

`x^2 + 20 - 2x= 0`

`x^2 -2x + 20 = 0`

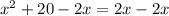
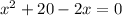
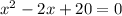
Given a quadratic equation of the form
`ax^2 +bx + c = 0`

The quadratic formula is as follows;

`x = (-b \± √(b^2 - 4ac))/(2a)`

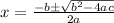
Where a = 1, b = -2 and c = 20

`x = (-b \± √(b^2 - 4ac))/(2a)`

`x = (-(-2) \± √((-2)^2 - 4*1*20))/(2 * 1)`

`x = (2 \± √(4 - 80))/(2)`

`x = (2 \± √(-76))/(2)`

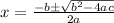
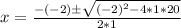
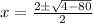
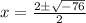
Factorize -76

`x = (2 \± √(-19 * 4))/(2)`

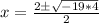
Split the square root

`x = (2 \± √(-19) *√(4))/(2)`

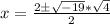
Square root of 4 is 2

`x = (2 \± √(-19) * 2)/(2)`

`x = (2 \± 2√(-19))/(2)`

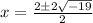
Split Fraction

`x = (2)/(2) \± (2√(-19))/(2)`

`x = 1 \ + √(-19)\ or\ x = 1 \ - √(-19)`

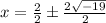
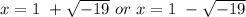
The expression can not be further simplified;

Hence,
`x = 1 \ + √(-19)\ or\ x = 1 \ - √(-19)`