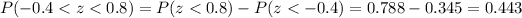Answer:
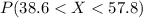
And we can assume a normal distribution and then we can solve the problem with the z score formula given by:
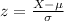
And replacing we got:
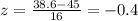
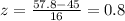
We can find the probability of interest using the normal standard table and with the following difference:
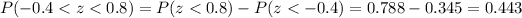
Explanation:
Let X the random variable who represent the expense and we assume the following parameters:
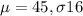
And for this case we want to find the percent of his expense between 38.6 and 57.8 so we want this probability:
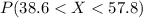
And we can assume a normal distribution and then we can solve the problem with the z score formula given by:
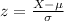
And replacing we got:
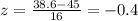
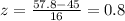
We can find the probability of interest using the normal standard table and with the following difference: