Question

Question 6(Multiple Choice Worth 3 points) (03.05 MC) Find the domain for the rational function f of x equals quantity x plus 1 end quantity divided by quantity x minus 2 end quantity. (−[infinity], 2) (2, [infinity]) (−[infinity], −2) (−2, [infinity]) (−[infinity], 1) (1, [infinity]) (−[infinity], −1) (−1, [infinity])

Answer 1

Answer: A (-infinity,2) (2,infinity)

Explanation:

Answer 2

(A)
`(-\infty, 2)(2, \infty)`

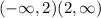
(−[infinity], 2) (2, [infinity])

Explanation:

Given the rational function, f(x) such that:

`f(x)=(x+1)/(x-2)`

The domain of the function are the values of x for which f(x) is defined.

A rational function is undefined when its denominator equals zero.

Denominator of f(x)=x-2

x-2=0

x=2

Therefore, f(x) is undefined at x=2.

The domain of f(x) is all therefore all real numbers excluding 2.

This is written in set notation as:

`(-\infty, 2)(2, \infty)`

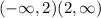
The correct option is A.