Answer:
(a) The probability that a male is selected, then two females is 0.4352.
(b) The probability that a female is selected, then two males is 0.3348.
(c) The probability that two females are selected, then one male is 0.4352.
(d) The probability that three males are selected is 0.0717.
(e) The probability that three females are selected is 0.1583.
Explanation:
We are given that a math class consists of 25 students, 14 female and 11 male. Three students are selected at random to participate in a probability experiment.
(a) The probability that a male is selected, then two females is given by;
Number of ways of selecting a male from a total of 11 male =
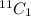
Number of ways of selecting two female from a total of 14 female =
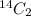
Total number of ways of selecting 3 students from a total of 25 =
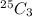
So, the required probability =
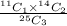
=
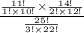 {
{
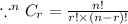 }
}
=
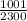 = 0.4352
= 0.4352
(b) The probability that a female is selected, then two males is given by;
Number of ways of selecting a female from a total of 14 female =
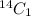
Number of ways of selecting two males from a total of 11 male =
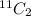
Total number of ways of selecting 3 students from a total of 25 =
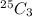
So, the required probability =
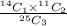
=
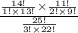 {
{
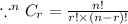 }
}
=
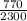 = 0.3348
= 0.3348
(c) The probability that two females is selected, then one male is given by;
Number of ways of selecting two females from a total of 14 female =
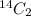
Number of ways of selecting one male from a total of 11 male =
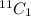
Total number of ways of selecting 3 students from a total of 25 =
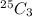
So, the required probability =
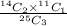
=
 {
{
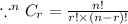 }
}
=
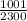 = 0.4352
= 0.4352
(d) The probability that three males are selected is given by;
Number of ways of selecting three males from a total of 11 male =

Total number of ways of selecting 3 students from a total of 25 =
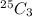
So, the required probability =
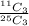
=
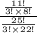 {
{
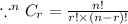 }
}
=
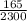 = 0.0717
= 0.0717
(e) The probability that three females are selected is given by;
Number of ways of selecting three females from a total of 14 female =
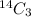
Total number of ways of selecting 3 students from a total of 25 =
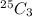
So, the required probability =

=
 {
{
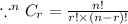 }
}
=
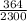 = 0.1583
= 0.1583