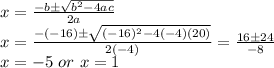Question

3) Equation 3 should represent a parabola that is a vertical stretch of the parent function and has a y-intercept greater than 3 and opens down. Equation 3:___________________________________________________________________ What strategy are you using to solve this equation and why? ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ Show your work and solution for solving this equation:

Answer 1

The answer is given below

Explanation:

The equation of a quadratic function is given by:

ax² + bx + c where a, b and c are the coefficients of the quadratic equation. The value of a determines whether the graph opens up or down (if a is positive opens up and if a is negative opes down), the value of c determines the y intercept (if c is positive, we have a positive intercept and if c is negative the intercept is negative).

The chosen equation is -x² -4x + 5. Since it has y-intercept of 5 and opens down (coefficient of x² is -1)

Let us assume a vertical stretch of 4, the new equation becomes:

4(-x² -4x + 5)

-4x² - 16x + 20

-4x² - 16x + 20 = 0

a = -4, b = -16 and c = 20

Using the quadratic formula:

`x=(-b \pm √(b^2-4ac) )/(2a)\\ x=(-(-16) \pm √((-16)^2-4(-4)(20)) )/(2(-4))=(16 \pm 24)/(-8) \\x= -5 \ or \ x=1`