Question

6. Find the variance and standard deviation for the given data using the formula. Round your answer to one more decimal place than the original data g

Answer 1

Answer and Step-by-step explanation:

Variance is the measurement of the spread bewteen the numbers of the data set and can be calculated by the formula:

σ² = ∑(x - ⁻x)² / n

1) With the data, find its mean (⁻x) by adding all the values and dividing the sum by total number of elements the data has;

2) Subtract each value of the data to the mean;

3) Square the result of the subtractions;

4) Add the squares;

5) Divide the sum by the total number of elements of the set;

6) The result is the Variance (σ²);

Standard Deviation is the measure of how far the values of the data set are from the mean and it is the square root of Variance:

σ =
`\sqrt{(variance)^(2)}`

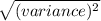
So, to calculate standard deviation, you just take the square root of the variance.