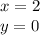1 Answer

Berkeley · Answer 1 · 2021-06-13T16:12:43+0000

Answer:

See steps below on how to obtain the final solution

$x=2\\y=0$

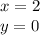
using Gauss elimination

Explanation:

Let's write this system with the equations swapped since we want the largest value for the x dependence in the top row:

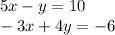
$5x-y=10\\-3x+4y=-6$

Now let's scale the first equation by dividing it by 5 (the leading coefficient for x):

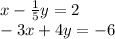
$x-(1)/(5) y=2\\-3x+4y=-6$

now multiply row 1 by 3 and combine with row 2 :

$3\,x-(3)/(5) y=6\\-3x+4y=-6\\ \\0+(17)/(5) y=0$

now replace the second row by this combination:

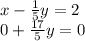
$x-(1)/(5) y=2\\0+(17)/(5) y=0$

Now multiply the second row by 5/17:

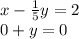
$x-(1)/(5) y=2\\0+} y=0$

multiply the bottom row by 1/5 and combine with the first row to eliminate the term in y:

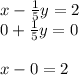
$x-(1)/(5) y=2\\0+(1)/(5) y=0\\ \\x-0=2$

Now we have the answer to the system:

$x=2\\y=0$

Please log in or register to add a comment.