Answer:
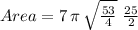
Explanation:
Let's use the integral formula for the surface area of revolution of the function y(x) around the x-axis, which is:
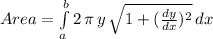
and which in our case, we can obtain the following:
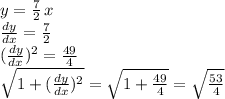
Recall as well that
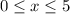 , which gives us the limits of integration:
, which gives us the limits of integration:

If we compare it with the geometry formula:
Lateral surface of cone =

which is exactly the expression we calculated with the integral.