Answer:
II quadrant.
Explanation:
Consider given function:
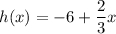
Here, we have to find the quadrant from which the graph of function is not passing.
For x=0,
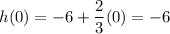
Thus, y-intercept is (0,-6).
For h(x)=0,

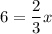

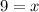
Thus, x-intercept is (9,0).
Plot (0,-6) and (9,0) on a coordinate plane and join them by a straight line as shown below.
From the graph it is clear that the graph is not passing through the II quadrant.
Therefore, the graph is not passing through the II quadrant.