Question

"Conservationists have despaired over destruction of tropical rain forest by logging, clearing, and burning." These words begin a report on a statistical study of the effects of logging in Borneo. Here are data on the number of tree species in 12 unlogged forest plots and 9 similar plots logged 8 years earlier:

Answer 1

The answer is "(0.461 , 7.206)"

Explanation:

In the given question some information is missing, that is data. so, the correct answer to this question can be defined as follows:

UnLogged:

`x_1=17.500\\s_1=3.529\\n_1=12`

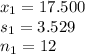
Logged:

`x_2=13.667\\ s_2=4.500\\n_2=9\\`

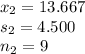
formula of std error:

`\ std \ error =\sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2)}`

`=\sqrt{(3.529^2)/(12)+(4.500^2)/(9)}\\\\=\sqrt{(3.529^2* 3+4.500^2* 4)/(36)}\\\\=1.8133`

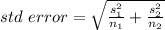
Point differential estimation =
`x_1-x _2`

`= 17.500-13.667\\=3.833`

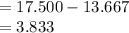
For 90 percent t= 1.860 Cl & 8 df

error of margin E =
`t* \ std \ error`

`= 1.860 * 1.8133\\= 3.373`

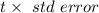
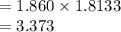
Lower bound =mean difference -E=0.461

Upper bound = mean difference+ E=7.206

In the above 90% confidence interval were the population mean= (0.461 , 7.206)