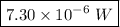Question

If 62.9 cm of copper wire (diameter = 1.15 mm, resistivity = 1.69 × 10-8Ω·m) is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 8.43 mT/s, at what rate is thermal energy generated in the loop?

Answer 1

The answer is "
`\bold{7.30 * 10^(-6)}`"

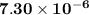Step-by-step explanation:

length of the copper wire:

L= 62.9 cm

r is the radius of the loop then:

`r=(L)/(2 \pi)\\`

`=(62.9)/(2* 3.14)\\\\=(62.9)/(6.28)\\\\=10.01\\`

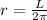
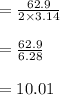
area of the loop Is:

`A_L= \pi r^2`

`=100.2001* 3.14\\\\=314.628`

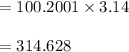
change in magnetic field is:

`=(dB)/(dt) \\\\ = 0.01\ (T)/(s)`

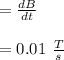
then the induced emf is:
`e = A_L * (dB)/(dt)`

`=314.628 * 0.01\\\\=3.14* 10^(-5)V`

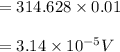
resistivity of the copper wire is:
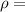`\rho =` 1.69 × 10-8Ω·m

diameter d = 1.15mm

radius (r) = 0.5mm

`= 0.5 * 10^(-3) \ m`

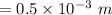
hence the resistance of the wire is:

`R=(\rho L)/(\pi r^2)\\`

`=(1.69 * 10^(-8)(62.9))/(3.14 * (0.5 * 10^(-3))^2)\\\\=(1.69 * 10^(-8)(62.9))/(3.14 * 0.5 * 0.5 * 10^(-6))\\\\=(1.69 * 10^(-8)(62.9))/(3.14 * 0.25 * 10^(-6))\\\\=135.41 * 10^(-2)\\=1.35* 10^(-4)\\`

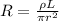
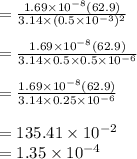
Power:

`P=(e^2)/(R)`

`=(3.14* 10^(-5)* 3.14* 10^(-5))/(1.35 * 10^(-4))\\\\=7.30 * 10^(-6)`

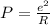
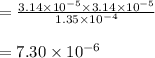
The final answer is:
`\boxed{7.30 * 10^(-6) \ W}`