Question

3. A 31.2-g piece of silver (s = 0.237 J/(g · °C)), initially at 277.2°C, is added to 185.8 g of a liquid, initially at 24.4°C, in an insulated container. The final temperature of the metal–liquid mixture at equilibrium is 28.3°C. What is the specific heat of the liquid? Neglect the heat capacity of the container.

Answer 1

`Cp_(liquid)=2.54(J)/(g\°C)`

Step-by-step explanation:

Hello,

In this case, since silver is initially hot as it cools down, the heat it loses is gained by the liquid, which can be thermodynamically represented by:

`Q_(Ag)=-Q_(liquid)`

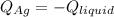
That in terms of the heat capacities, masses and temperature changes turns out:

`m_(Ag)Cp_(Ag)(T_2-T_(Ag))=-m_(liquid)Cp_(liquid)(T_2-T_(liquid))`

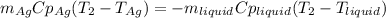
Since no phase change is happening. Thus, solving for the heat capacity of the liquid we obtain:

`Cp_(liquid)=(m_(Ag)Cp_(Ag)(T_2-T_(Ag)))/(-m_(liquid)(T_2-T_(liquid))) \\\\Cp_(liquid)=(31.2g*0.237(J)/(g\°C)*(28.3-227.2)\°C)/(185.8g*(28.3-24.4)\°C)\\ \\Cp_(liquid)=2.54(J)/(g\°C)`

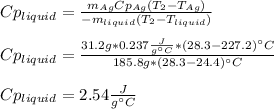
Best regards.