Question

A student wants to estimate the mean score of all college students for a particular exam. First use the range rule of thumb to make a rough estimate of the standard deviation of those scores. Possible scores range from 300 to 2200. Use technology and the estimated standard deviation to determine the sample size corresponding to a 90​% confidence level and a margin of error of 100 points. What​ isn't quite right with this​ exercise? The range. rule of thumb.estimate for the standard deviation. nothing.

Answer 1

See explanation below

Explanation:

range = 2200 - 300 = 1900

To find standard deviation, we have:

standard deviation = range/4 =
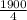`(1900)/(4)` = 475

The range rule of thumb estimate for the standard deviation is 475

Given:

Standard deviation,
`\sigma` = 475

Margin of Error, ME = 100

`\alpha` = 1 - 0.90 = 0.10

Za/2 = Z0.05 = 1.64

Find sample size, n:

n ≥
`[Z_\alpha_/_2 * ((\sigma)/(ME))]^2`

n ≥
`[1.64 * ((475)/(100))]^2`

n ≥ 60.68

≈ 61

Minimun sample size,n = 61