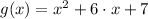Question

PLZZZZZ HLPPPPP MEEEEEEEEEE NOW <3

Answer 1

`g(x) = x^(2) + 6\cdot x + 7`

Explanation:

The blue parabola is only a translated version of the red parabola. The standard form of a vertical parabola centered at (h,k), that is, a parabola whose axis of symmetry is parallel to y-axis, is of the form:

`y - k = C\cdot (x-h)^(2)`

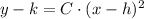
Where:

`h`,
`k` - Horizontal and vertical components of the vertex with respect to origin, dimensionless.

`C` - Vertex constant, dimensionless. (If C > 0, then vertex is an absolute minimum, but if C < 0, then vertex is an absolute maximum).

Since both parabolas have absolute minima and it is told that have the same shape, the vertex constant of the blue parabola is:

`C = 1`

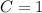
After a quick glance, the location of the vertex of the blue parabola with respect to the origin is:

`V(x,y) = (-3,-2)`

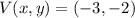
The standard form of the blue parabola is
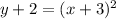`y+2 = (x+3)^(2)`. Its expanded form is obtained after expanding the algebraic expression and clearing the independent variable (y):

`y + 2 = x^(2) +6\cdot x + 9`

`y = x^(2) + 6\cdot x + 7`

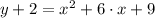
Then, the blue parabola is represented by the following equations:

`g(x) = x^(2) + 6\cdot x + 7`