Answer:
n = 10
Explanation:
Using the definition of n
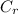 =
=
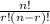
where n! = n(n - 1)(n - 2)..... × 3 × 2 × 1
Given
n
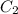 = 4n + 5 , then
= 4n + 5 , then
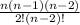 = 4n + 5
= 4n + 5
Cancel the terms from (n - 2).... on numerator/denominator
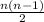 = 4n + 5 ( multiply both sides by 2 )
= 4n + 5 ( multiply both sides by 2 )
n² - n = 8n + 10 ( subtract 8n + 10 from both sides )
n² - 9n - 10 = 0 ← in standard form
(n - 10)(n + 1) = 0 ← in factored form
Equate each factor to zero and solve for n
n - 10 = 0 ⇒ n = 10
n + 1 = 0 ⇒ n = - 1
However n > 0 ⇒ n = 10