Question

To measure the takeoff performance of an airplane, the horizontal position of the plane was measured every second, from t = 0 to t = 12. the position in fee were: 0,8.8, 29.9, 62.0, 104.7, 159.1, 222.0, 294.5, 380.4, 471.1, 571.7, 686.8, and 809.2. Find the least squares cubic curve y = Bo + Bit + Bzt+ B3t for this data, then use the result to estimate the vel l ana when t= 4.5 seconds.

Answer 1

The value of y when t = 4.5 seconds is 130.31.

Explanation:

The data provided is:

S = {0, 8.8, 29.9, 62.0, 104.7, 159.1, 222.0, 294.5, 380.4, 471.1, 571.7, 686.8, and 809.2}

Use MATLAB to form the least squares cubic curve equation.

The codes are as follows:

t = [0:1:12]

y = [0,8.8,29.9,62.0,104.7,159.1,222.0,294.5,380.4,471.1,571.7,686.8,809.2];

txt =printf("The coeff of the curve in order of decreasing power are: ");

p = polyfit(t,y,3)

y1 = polyval(p,4.5)

The output is attached below.

The least squares cubic curve equation is:

`y = -0.855769 + 4.702485\cdot t + 5.555370\cdot t^(2)-0.027360\cdot t^(3)`

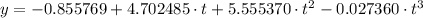
The value of y when t = 4.5 is:

`y = -0.855769 + 4.702485\cdot t + 5.555370\cdot t^(2)-0.027360\cdot t^(3)`

`= -0.855769 + (4.702485\cdot 4.5) + (5.555370\cdot 4.5^(2))-(0.027360\cdot 4.5^(3))\\=130.308476\\\approx 130.31`

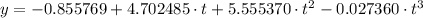
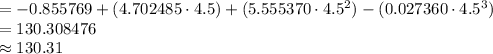
Thus, the value of y when t = 4.5 seconds is 130.31.