Question

Below are the jersey numbers of 11 players randomly selected from a football team. Find the​ range, variance, and standard deviation for the given sample data. What do the results tell​ us? 40 39 8 82 25 53 97 1 28 41 94

Answer 1

(a)Range = 96

(b)Variance=1059.36

(c)Standard Deviation =32.55

Explanation:

(a)Range

• Highest Value = 97
• Lowest Value = 1

Range = Highest Value - Lowest Value

=97-1

=96

(b)Variance

The variance of a sample for ungrouped data is defined by the formula:

`Variance, s^2 = \frac{\sum(x-\overline{x})^2}{n-1}`

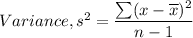
First, we determine the mean of the sample data.

`Mean = (40 +39+ 8+ 82+ 25+ 53+ 97+ 1+ 28+ 41+ 94)/(11) \\=(508)/(11)\\\\ \overline{x}=46.2`

`\sum(x-\overline{x})^2=(40-46.2)^2 +(39-46.2)^2+ (8-46.2)^2+ (82-46.2)^2+ (25-46.2)^2+ (53-46.2)^2+ (97-46.2)^2+ (1-46.2)^2+ (28-46.2)^2+ (41-46.2)^2+ (94-46.2)^2\\\\=38.44+51.84+1459.24+1281.64+449.44+46.24+2580.64+2043.04+331.24+27.04+2284.84`

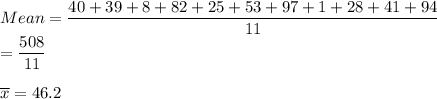
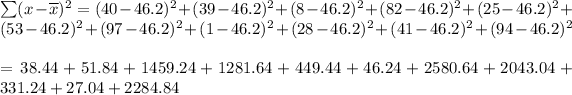
=10593.64

Therefore:

Variance, Variance,

`Variance, s^2 = (10593.64)/(11-1)\\\\=1059.36`

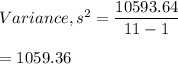
(c)Standard Deviation

`s=√(Variance)\\ =√(1059.36)\\s=32.55`

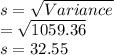
The results tell us that there is great variability in the number of jerseys of the player as evidenced by the high standard deviation and range.