Question

Use the given degree of confidence and sample data to construct interval for the population proportion. Of 369 randomly selected medical students, 23 said that they planned to work in a rural community. Construct a 95% confidence interval for the percentage of all medical students who plan to work in a rural community. (4.16%, 8.30%) (3.77%, 9.47%) (3.30%, 9.17%) (2.99%, 9.47%) (3.77%, 8.70%) In a poll of registered voters nationwide, 43% of those polled blamed of companies the most for the recent increase in gasoline prices. The margin of error at the 96% confidence level for this point estimate is 2.4%. Construct a 95% confidence level for the population proportion who blame oil companies for the recent increase in gasoline prices. (0.382, 0.478) (0.368, 0.492) (0.406, 0.477) (0.383, 0.477) Cannot be determined from the information given.

Answer 1

e) (3.77%, 8.70%)

95% confidence interval for the percentage of all medical students who plan to work in a rural community

(3.83% , 8.69%)

95% confidence level for the population proportion who blame oil companies for the recent increase in gasoline prices

(0.406 , 0.454)

Explanation:

Step(i):-

Given random sample size 'n' = 369

Sample proportion

`p = (x)/(n) = (23)/(369) = 0.0623`

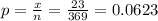
95% confidence intervals are determined by

`(p^(-) - Z_(0.05) \sqrt{(p(1-p))/(n) } , p^(-) + Z_(0.05) \sqrt{(p(1-p))/(n) })`

`(0.0623 - 1.96 \sqrt{(0.0623(1-0.0623))/(369) } , 0.0623 + 1.96\sqrt{(0.0623(1-0.0623))/(369) })`

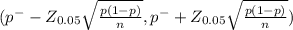
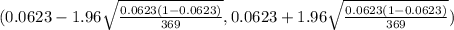
(0.0623 - 0.0246 , 0.0623 + 0.0246)

(0.0383 , 0.0869)

(3.83% , 8.69%)

95% confidence interval for the percentage of all medical students who plan to work in a rural community

(3.83% , 8.69%)

Step(ii):-

Given 43% of those polled blamed of companies the most for the recent increase in gasoline prices

sample proportion 'p' = 0.43

Given Margin of error (M.E) = 0.024

95% confidence intervals are determined by

`(p^(-) - Z_(0.05) \sqrt{(p(1-p))/(n) } , p^(-) + Z_(0.05) \sqrt{(p(1-p))/(n) })`

`(0.43 - 0.024 } , 0.43 +0.024 )`

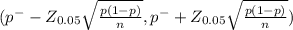
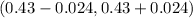
(0.406 , 0.454)

Final answer:-

95% confidence level for the population proportion who blame oil companies for the recent increase in gasoline prices

(0.406 , 0.454)