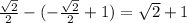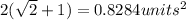Question

Please help The answer is 0.8284 unit2.

Answer 1

Answer: 0.8284 units²

Explanation:

To find the area between curves, we need to use the integral. We can see that both sides of the shaded region are equal to each other. Therefore, we can find the area of one shaded part and multiply it by 2 for the 2 shaded regions. For the integral, we can find the area of the shaded region on the left side, on the interval from 0 to π/4.

Now that we know the integral, we can figure out the function. We do this by subtracting the top curve by the bottom curve. The top curve on the left shaded region, is y=cosx. The bottom curve on the shaded region is y=sinx. Therefore, we will subtract cosx-sinx.

`2\int\limits^(\pi )/(4) _0 {cosx-sinx} \, dx`

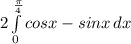
Now that we have the integral, we can solve by splitting the integral into 2 separate integrals by the Sum Rule. Let's disregard the multiply by 2 for now, but we will make sure to multiply by 2 at the end.

`\int\limits^(\pi )/(4) _0 {cosx} \, dx -\int\limits^(\pi )/(4) _0 {sinx} \, dx`

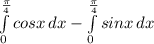
Now, we can solve each integral separately.

`\int\limits^(\pi )/(4) _0 {cosx} \, dx =sinx]^\pi^ /^40`

*Note: The 0 is at the base of the bracket. I can't find a way to do it in the equation editor, but know that it's there.

`sin((\pi )/(4) )-sin(0)=(√(2) )/(2) -0=(√(2) )/(2)`

Now, we can find the integral of sinx.

`\int\limits^(\pi )/(4) _0 {sinx} \, dx=-cos]^\pi ^/^40`

*Note: The 0 is at the base of the bracket. I can't find a way to do it in the equation editor, but know that it's there.

`-cos((\pi )/(4) )-(-cos(0))=-(√(2) )/(2) -(-1)=-(√(2) )/(2) +1`

Now that we have the integral of each integral, we can subtract them, and multiply by 2.

`(√(2) )/(2) -(-(√(2) )/(2) +1)=√(2)+1`

`2(√(2) +1)=0.8284 units^2`