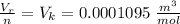Question

We have air (21% O2 and 79% N2) at 23 bar and 30 C. 4. What is the ideal molar volume (m^3/kmol)? a. b. What is the Z factor? What is the real molar volume?

Answer 1

The ideal molar volume is
`(V)/(n) =V_z= 0.001095 \ m^3/mol`

The Z factor is
`Z = 0.09997`

The real molar volume is
`(V_r)/(n) = V_k= 0.0001095\ (m^3)/(mol)`

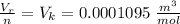
Step-by-step explanation:

From the question we are told that

The pressure is
`P = 23 \ bar = 23 *10^5 Pa`

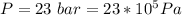
The temperature is
`T = 30 ^ oC = 303 \ K`

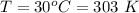
According to the ideal gas equation we have that

`PV = nRT`

=>
`(V)/(n)=V_z= (RT)/(P)`

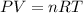
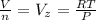
Where
`(V)/(n )` is the molar volume and R is the gas constant with value

`R = 8.314 \ m^3 \cdot Pa \cdot K^(-1)\cdot mol^(-1)`

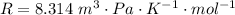
substituting values

`(V)/(n) =V_z= ( 8.314 * 303)/(23 *10^(5))`

`(V)/(n) =V_z= 0.001095 \ m^3/mol`

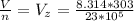
The compressibility factor of the gas is mathematically represented as

`Z = (P * V_z)/(RT)`

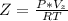
substituting values

`Z = (23 *10^(5) * 0.001095)/(8.314 * 303)`

`Z = 0.09997`

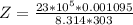
Now the real molar volume is evaluated as

`(V_r)/(n) = V_k= (Z * RT )/(P)`

substituting values

`(V_r)/(n) = V_k= (0.09997 * 8.314 * 303)/(23 *10^(5))`

`(V_r)/(n) = V_k= 0.0001095\ (m^3)/(mol)`