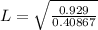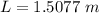Answer:
The length of the rod for the condition on the question to be met is
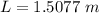
Step-by-step explanation:
The Diagram for this question is gotten from the first uploaded image
From the question we are told that
The mass of the rod is
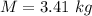
The mass of each small bodies is
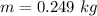
The moment of inertia of the three-body system with respect to the described axis is
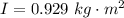
The length of the rod is L
Generally the moment of inertia of this three-body system with respect to the described axis can be mathematically represented as
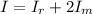
Where
 is the moment of inertia of the rod about the describe axis which is mathematically represented as
is the moment of inertia of the rod about the describe axis which is mathematically represented as
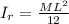
And
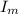 the moment of inertia of the two small bodies which (from the diagram can be assumed as two small spheres) can be mathematically represented as
the moment of inertia of the two small bodies which (from the diagram can be assumed as two small spheres) can be mathematically represented as
![I_m = m * [\frac{L} {2} ]^2 = m* (L^2)/(4)](https://img.qammunity.org/2021/formulas/physics/college/oyr0dslbofblybs9ohjdmjmvxobq4wqdqd.png)
Thus
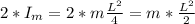
Hence
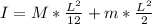
=>
![I = [(M)/(12) + (m)/(2)] L^2](https://img.qammunity.org/2021/formulas/physics/college/i11frq08c9qrhiqh59ct5vv8fzdwxdggma.png)
substituting vales we have
![0.929 = [(3.41)/(12) + (0.249)/(2)] L^2](https://img.qammunity.org/2021/formulas/physics/college/wpajpcohcg97sgqu3z371bhcu3n24rm85l.png)