Question

Would you need to use the chain rule to find the derivative of this function?

Answer 1

TRUE. We need to use the chain rule to find the derivative of the given function.

Explanation:

Chain rule to find the derivative,

We have to find the derivative of F(x)

If F(x) = f[g(x)]

Then F'(x) = f'[g(x)].g'(x)

Given function is,

y =
`√(2x+3)`

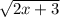
Here g(x) = (2x + 3)

and f[g(x)] =
`√(2x+3)`

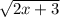
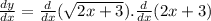
`(dy)/(dx)=(d)/(dx)(√(2x+3)).(d)/(dx) (2x+3)`

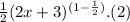
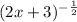
y' =
`(1)/(2)(2x+3)^{(1-(1)/(2))}.(2)`

=
`(2x+3)^{-(1)/(2)}`

y' =
`(1)/(√(2x+3))`

Therefore, it's true that we need to use the chain rule to find the derivative of the given function.