Question

A woman who weighs 500 N stands on an 8 m long board that weighs 100 N. The board is supported at each end. The support force at the right end is 3 times bigger than the support force at the left end. How far from the right end is the woman standing

Answer 1

`1.6\; \rm m`.

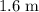Step-by-step explanation:

Let
`x` denote the distance (in meters) between the person and the right end of the board.

To keep the calculations simple, consider another unknown: let
`y` denote the support force (in Newtons) on the left end. The support force on the right end of this board would be
`3 \, y` (also in Newtons.)

Now there are two unknowns. At least two equations will be required for finding the exact solutions. For that, consider this board as a lever, but with two possible fulcrums. Refer to the two diagrams attached. (Not to scale.)

• In the first diagram, the support at the left end of the board is considered as the fulcrum.
• In the second diagram, the support at the right end of the board is considered as the fulcrum.

Calculate the torque in each situation. Note that are four external forces acting on this board at the same time. (Two support forces and two weights.) Why does each of the two diagrams show only three? In particular, why is the support force at each "fulcrum" missing? The reason is that any force acting on the lever at the fulcrum will have no direct impact on the balance between torques elsewhere on the lever. Keep in mind that the torque of each force on a lever is proportional to
`r`, the distance between the starting point and the fulcrum. Since that missing support force starts right at the fulcrum, its
`r` will be zero, and it will have no torque in this context.

Hence, there are three (non-zero) torques acting on the "lever" in each diagram. For example, in the first diagram:

• The weight of the board acts at the center of the board,
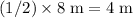  `(1/2) * 8\; \rm m = 4\; \rm m` from the fulcrum. This force will exert a torque of
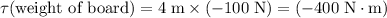  `\tau(\text{weight of board}) = 4\; \rm m * (-100\; \rm N) = (-400\; \rm N \cdot m)` on this "lever". The negative sign indicates that this torque points downwards.

• The weight of the person acts at
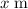  `x\;\rm m` from the right end of the board, which is
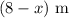  `(8 - x)\; \rm m` from the fulcrum at the other end of this board. This force will exert a torque of
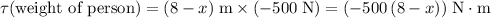  `\tau(\text{weight of person}) = (8 - x)\; {\rm m * (-500\; \rm N)} = (-500\, \mathnormal{(8 - x)})\; \rm N \cdot m` on this "lever". This torque also points downwards.

• The support on the right end of the board acts at
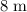  `8\; \rm m` from the fulcrum (i.e., the left end of this board.) This force will exert a torque of
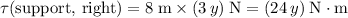  `\tau(\text{support, right}) = 8\; {\rm m} * (3\, \mathnormal{y})\; {\rm N} = (24\, y)\; \rm N \cdot m` on the "lever". This torque points upwards.

If the value of
`x` and
`y` are correct, these three torques should add up to zero. That is:

`\underbrace{(-400)}_{\text{board}} + \underbrace{(-500\, (8 - x))}_{\text{person}} + \underbrace{24\, y}_{\text{support}} = 0`.

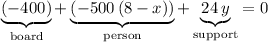That gives the first equation of this system. Similarly, a different equation can be obtained using the second diagram:

`\underbrace{(-400)}_{\text{board}} + \underbrace{(-500\,x)}_{\text{person}} + \underbrace{8\, y}_{\text{support}} = 0`.

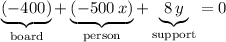Combine these two equations into a two-by-two system. Solve the system for
`x` and
`y`:

`\left\lbrace\begin{aligned}&x = 1.6\\ &y = 150\end{aligned}\right.`.

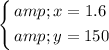In other words, the person is standing at about
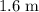`1.6\; \rm m` from the right end of the board. The support force at the left end of the board is
`150\; \rm N`.