Question

An investment of ​$110 comma 000110,000 was made by a business club. The investment was split into three parts and lasted for one year. The first part of the investment earned​ 8% interest, the second​ 6%, and the third​ 9%. Total interest from the investments was $ 8280.$8280. The interest from the first investment was 22 times the interest from the second. Find the amounts of the three parts of the investment.

Answer 1

X = amount invested in 8% interest = $54000

Y =amount invested in 6% interest = $36000

Z = amount invested in 9% interest = $20000

Step-by-step explanation:

Given that:

The amount of investment = $110,000

The investment was split into three parts and lasted for one year.

The first part of the investment earned​ 8% interest

The Second part of the investment earned​ 6% interest

The third part of the investment earned​ 9% interest

Total interest from the investments was $ 8280.

The interest from the first investment was 2 times the interest from the second.

The objective is to find the amounts of the three parts of the investment.

Let XYZ be the first,second and third part of the investment earned respectively.

So; we can say :

X + Y + Z = 110000 --------- (1)

From the total amount of interest from the investment; we have :

`X((8)/(100)) + Y ((6)/(100)) + Z( (9)/(100)) = 8280`

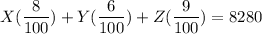
0.08 X + 0.06 Y + 0.09 Z = 8280 -------- (2)

Similarly; let's not forget that the interest from the first investment was 2 times the interest from the second investment.

So;

0.08 X = 2(0.06 )Y

0.08 X = 0.12 Y

0.08 X - 0.12 Y = 0 ------------ (3)

From equation (3); let make X, the subject of the formula; by doing so, we have:

0.08 X - 0.12 Y = 0

0.08 X = 0.12 Y

`X = ((0.12 )/(0.08))Y`

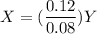
X = 1.5Y

Replace the value of X into equation (1), we have :

X + Y + Z = 110000 --------- (1)

1.5Y + Y + Z = 110000

2.5Y + Z = 110000 ------- (4)

Replace the value of X = 1.5Y into equation (2), we have :

0.08 X + 0.06 Y + 0.09 Z = 8280 -------- (2)

0.08(1.5 Y) + 0.06 Y + 0.09 Z = 8280

0.12 Y + 0.06 Y +0.09 Z = 8280

0.18 Y + 0.09 Z = 8280 ----- (5)

By Elimination method; we can determine the value of Y from equation 4 and 5 as follows:

Let's multiply Z by (0.09) in equation (4);

2.5Y + Z = 110000

-

0.18 Y + 0.09 Z = 8280

So;

0.225Y + 0.09Z = 9900

-

0.18 Y + 0.09 Z = 8280

0.045 Y + 0 = 1620

0.045 Y = 1620

Y = 1620/0.045

Y = 36000

From;

X = 1.5Y

X = 1.5 ( 36000)

X = 54000

From equation (1)

X + Y + Z = 110000 --------- (1)

54000 + 36000 + Z = 110000

Z = 110000 - 54000 - 36000

Z = 20000

Hence;

X = amount invested in 8% interest = $54000

Y =amount invested in 6% interest = $36000

Z = amount invested in 9% interest = $20000