Question

3. Two spherical objects at the same altitude move with identical velocities and experience the same drag force at a time t. If Object 1 has twice (2x) the diameter of Object 2, which object has the larger drag coefficient? Explain your answer using the drag equation.

Answer 1

Object 2 has the larger drag coefficient

Step-by-step explanation:

The drag force, D, is given by the equation:

`D = 0.5 c \rho A v^2`

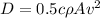
Object 1 has twice the diameter of object 2.

If
`d_2 = d`

`d_1 = 2d`

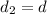
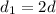
Area of object 2,
`A_2 = (\pi d^2 )/(4)`

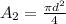
Area of object 1:

`A_1 = (\pi (2d)^2 )/(4)\\A_1 = \pi d^2`

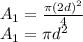
Since all other parameters are still the same except the drag coefficient:

For object 1:

`D = 0.5 c_1 \rho A_1 v^2\\D = 0.5 c_1 \rho (\pi d^2) v^2`

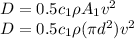
For object 2:

`D = 0.5 c_2 \rho A_2 v^2\\D = 0.5 c_2 \rho (\pi d^2/4) v^2`

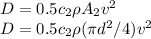
Since the drag force for the two objects are the same:

`0.5 c_1 \rho (\pi d^2) v^2 = 0.5 c_2 \rho (\pi d^2/4) v^2\\4c_1 = c_2`

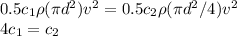
Obviously from the equation above, c₂ is larger than c₁, this means that object 2 has the larger drag coefficient