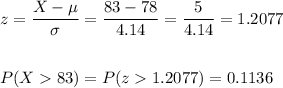Question

Decide whether you can use the normal distribution to approximate the binomial distribution. If you​ can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you​ cannot, explain why and use the binomial distribution to find the indicated probabilities. A survey of adults found that 78​% of those who text on cell phones receive spam or unwanted messages. You randomly select 100 adults who text on cell phones.

Requried:
a. Determine whether a normal distribution can be used to approximate the binomial distribution.
b. Sketch the graph of the normal distribution with the indicated probability shaded.
c. Find the probability that the number of people who receive spam or unwanted messages is at least 83.

Answer 1

a) It can be approximated by the normal distribution

b) Attached

c) P(X>83)=0.1136

Explanation:

The requirement to approximate the binomial distribution by a normal distribution is that both the products np and n(1-p) are greater than 10 for the sample size.

In this case, the sample size is n=100 and the probability of success is p=0.78.

We can verify the requirement as:

`np=100\cdot 0.78=78\\\\n(1-p)=100\cdot0.22=22`

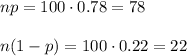
The requirement is satisfied, so the binomial can be approximated to a normal distribution.

The parameters of the normal distribution will be:

`\mu=np=100\cdot0.78=78\\\\\sigma=√(np(1-p))=√(100\cdot 0.78\cdot 0.22)=√(17.16)=4.14`

We can calculate the probability that the number of people who receive spam or unwanted messages is at least 83 using the z-score for X=83 and calculate the probability using the standard normal distribution:

`z=(X-\mu)/(\sigma)=(83-78)/(4.14)=(5)/(4.14)=1.2077\\\\\\P(X>83)=P(z>1.2077)=0.1136`