Question

Brenda, Anthony, and C are accused of During the interrogation they make the following claims:

Brenda says: "If Anthony is guilty then Charles is guilty too".
Anthony says: "Brenda did it and Charles is innocent".
Charles says: "I did not do it. One of the others, or maybe both of them did it"

Requried:
a. Write a formula in CNF that represents the conjunction of the three above claims using the following atomic propositions:

1. Brenda is guilty.
2. Anthony is guilty.
3. Charles is guilty

b. Are the three above statements contradictory?
c. Assuming that all of them are guilty, who lied during the interrogation? Justify.
d. Assuming that nobody lied, who is innocent and who is guilty? Justify.

Answer 1

Following are the answer to this question:

Step-by-step explanation:

Let,

A = Brenda is guilty.

B =Anthony is guilty.

C = Charles is guilty.

The Brenda says that If A then C:
`A\longrightarrow C`

The Anthony says that B and C are not:
`B \ \&\& \ \bar C`

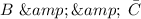
The Charles syas that
`\bar C \ \&\& (A || B ||(A \&\& B))`

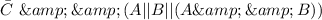
In option a)

The propositional logic formula as follows:

`A\Rightarrow C:\bar A \vee C\\B \&\& \bar C:B\wedge \bar C\\\bar C \&\&(A||B||(A\&\& B):\bar C\wedge (A\vee B\vee(A \wedge B))`

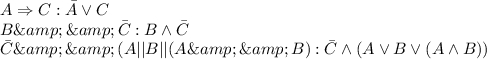
follows are the given claims:

`\bar A\vee C\\B \wedge \bar C\\\bar C\wedge (A\vee (A\wedge B)\vee B \vee (A \wedge B)) = \bar C \wedge (A \vee B)`

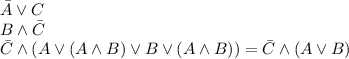
That's why the above code is false.

In option b)

In this option the given point is not contradictory because all three given point can't be satisfied.

In option c)

In this point A and C both were false because both lies that their claim are not satisfied.

In option d)

B equals to T, that's is A"Brenda is guilty".