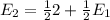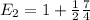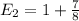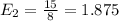Question

7.1 A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then she wins one-half of the value that appears on the die. Determine her expected winnings.

Answer 1

1.875

Explanation:

To find the expected winnings, we need to find the probability of all cases possible, multiply each case by the value of the case, and sum all these products.

In the die, we have 6 possible values, each one with a probability of 1/6, and the value of each output is half the value in the die, so we have:

`E_1 = (1)/(6)(1)/(2) + (1)/(6)(2)/(2) +(1)/(6)(3)/(2) +(1)/(6)(4)/(2) +(1)/(6)(5)/(2) +(1)/(6)(6)/(2)`

`E_1 = (1)/(12)(1+2+3+4+5+6)`

`E_1 = (21)/(12) = (7)/(4)`

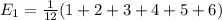
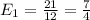
Now, analyzing the coin, we have heads or tails, each one with 1/2 probability. The value of the heads is 2 wins, and the value of the tails is the expected value of the die we calculated above, so we have:

`E_2 = (1)/(2)2 + (1)/(2)E_1`

`E_2 = 1 + (1)/(2)(7)/(4)`

`E_2 = 1 + (7)/(8)`

`E_2 = (15)/(8) = 1.875`