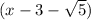Answer:
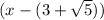 or
or
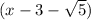 is a factor of the given polynomial.
is a factor of the given polynomial.
Explanation:
Let us learn the concept with an example first.
Let the polynomial be a quadratic function
 .
.
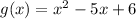
The roots of
 are 2 and 3.
are 2 and 3.
Putting
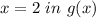

Putting
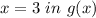
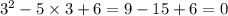
Putting x = 2 or x = 3, g(x) = 0
 The roots of equation g(x) are 2 and 3.
The roots of equation g(x) are 2 and 3.
Now, let us try to factorize g(x):
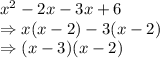
so, the equation can be written as:
 where 3 and 2 are the roots of equation.
where 3 and 2 are the roots of equation.
The factors are (x-3) and (x-2).
 for the polynomial f(x) which has roots
for the polynomial f(x) which has roots
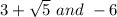 will have a factor:
will have a factor:
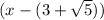 or
or