Question

Ava's bacteria population is modeled by an equation. Chase models his bacteria

population with a graph. Ava says that on day 14, she will have more bacteria than Chase
Is she right? Why or why not?

Answer 1

D

Explanation:

Trust

Answer 2

P(Chase) > P(Ava)

700 > 587

Therefore, Ava's claim is wrong!

On day 14, Chase's bacteria population will be greater than Ava's bacteria population.

Explanation:

Please refer to the attached image.

Ava's bacteria population is modeled by the following equation.

`$ b(t) = 200(1+0.08)^t $`

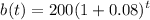
Where t is time in days and b(t) is the population of the bacteria after t days.

The graph represents the population of Chase's bacteria.

Ava claims that on day 14, she will have more bacteria than Chase.

Let us compare the population of both bacteria.

Chase bacteria population when t = 14 days:

From the graph, the population is approximately 700 at t = 14 days

P(Chase) ≈ 700

Ava bacteria population when t = 14 days:

at t = 14 days

`b(t) = 200(1+0.08)^t \\\\ b(14) = 200(1.08)^(14) \\\\ b(14) = 200 (2.93719)\\\\ b(14) = 587.44`

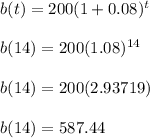
So, the population is approximately 587 at t = 14 days

P(Ava) ≈ 587

P(Chase) > P(Ava)

700 > 587

Therefore, Ava's claim is wrong!

On day 14, Chase's bacteria population will be greater than Ava's bacteria population.