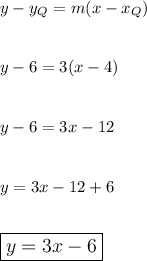Question

For the triangle with vertices P(-2,0), Q(4,6) and R(5,-3), find an equation for the median from

a) Vertex P
b) Vertex Q

Answer 1

Answer:
`\bold{a)\ y=(9)/(7)x+(18)/(7)}`

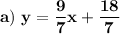
b) y = 3x - 6

Explanation:

Median is the line from the Vertex to the Midpoint of the opposite side

a)

Step 1: Find the Midpoint of QR:

Q = (4, 6) R = (5, -3)

`x_M=(x_Q+x_R)/(2)\qquad \qquad \qquad y_M=(y_Q+y_R)/(2)\\\\\\x_M=(4+5)/(2)\qquad \qquad \qquad \qquad y_M=(6+(-3))/(2)\\\\\\x_M=(9)/(2) \qquad \qquad \qquad \qquad \qquad y_M=(3)/(2)`

`Midpoint_(QR)=\bigg((9)/(2),(3)/(2)\bigg)`

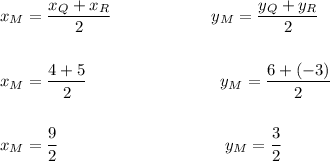
Step 2: Find the slope (m) for P (-2,0) to Midpoint of QR:

`m=(y_2-y_1)/(x_2-x_1)\\\\\\m=((9)/(2)-0)/((3)/(2)-(-2))\\\\\\m=((9)/(2))/((7)/(2))\\\\\\m=\bigg{(9)/(7)}`

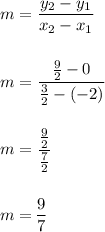
Step 3: Find the equation of the line from P to Midpoint of QR:

`y-y_P=m(x-x_P)\\\\\\y-0=(9)/(7)\bigg(x-(-2)\bigg)\\\\\\\\\large\boxed{y=(9)/(7)x+(18)/(7)}`

**************************************************************************************

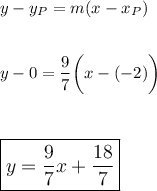
b)

Step 1: Find the Midpoint of PR:

P = (-2, 0) R = (5, -3)

`x_M=(x_P+x_R)/(2)\qquad \qquad \qquad y_M=(y_P+y_R)/(2)\\\\\\x_M=(-2+5)/(2)\qquad \qquad \qquad \qquad y_M=(0+(-3))/(2)\\\\\\x_M=(3)/(2) \qquad \qquad \qquad \qquad \qquad y_M=-(3)/(2)`

`Midpoint_(PR)=\bigg((9)/(2),(3)/(2)\bigg)`

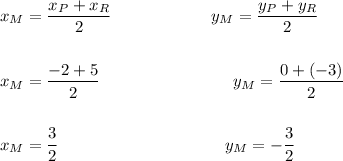
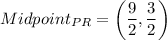
Step 2: Find the slope (m) for Q (4,6) to Midpoint of PR:

`m=(y_2-y_1)/(x_2-x_1)\\\\\\m=(6-(-(3)/(2)))/(4-((3)/(2)))\\\\\\m=((15)/(2))/((5)/(2))\\\\\\m=\bigg{3}`

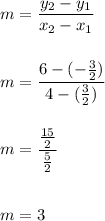
Step 3: Find the equation of the line from Q to Midpoint of PR:

`y-y_Q=m(x-x_Q)\\\\\\y-6=3(x-4)\\\\\\y-6=3x-12\\\\\\y=3x-12+6\\\\\\\large\boxed{y=3x-6}`