Answer:
Area of ABCD = 959.93 units²
Explanation:
a). By applying Sine rule in the ΔABD,
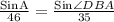
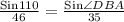
Sin∠DBA =
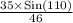
m∠DBA =
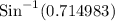
m∠DBA = 45.64°
Therefore, m∠ADB = 180° - (110° + 45.64°) = 24.36°
m∠ADB = 24.36°
c). Area of ABCD = Area of ΔABD + Area of ΔBCD
Area of ΔABD = AD×BD×Sin(
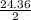 )
)
= 35×46Sin(12.18)
= 339.68 units²
Area of ΔBCD = BD×BC×Sin(
 )°
)°
= 46×27×(0.4994)
= 620.25 units²
Area of ABCD = 339.68 + 620.25
= 959.93 units²