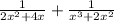Answer:
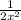
Explanation:
When you add fractions, the fractions must have common denominators.
Multiply the denominators together to get a common denominator.
(2
 +4x) by (
+4x) by (
 +2
+2
 ) =
) =
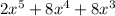
This is the common denominator.
However, you also need to multiply the numerators.
For example,
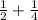
2 times 4 is 8.
But 1/8 + 1/8 isn't the answer. Thats 2/8 or 1/4.
If you multiply 1 by 4 and 2 by 1, however, you'll get the correct answer.
Multiply 1 by x^3 + 2x^2 and 1 by 2x^2 + 4x.
This results in:
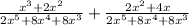
Since they have a common denominator, you can just put the numbers over one denominator like:
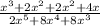
Both the and numerators can be factored.
The numerator can be factored into x
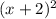 .
.
The denominator can be factored into
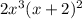
Like:
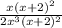
The (x+2)^2 cancel, leaving:
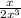
Which is basically:
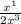
Which simplifies to
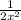
Like this?: